Fraktale – Im Kleinen wie im Großen

Auch in der Natur kommen selbstähnliche Objekte vor

Geometrische Figuren, die sich aus verkleinerten Versionen ihrer selbst zusammensetzen, nennt man Fraktale.
Vergrößert man also einen Ausschnitt eines Fraktals beliebig stark, so bleibt seine Geometrie trotzdem gleich
(Selbstähnlichkeit). Ein bekanntes Fraktal ist die nach einem Mathematiker benannte Mandelbrot-Menge, hier als
durchscheinender Hintergrund dargestellt. Fraktale tauchen aber nicht nur in der Mathematik auf, auch in
unserer Umwelt gibt es Objekte mit fraktalem Aufbau. Forschende des Max-Planck-Instituts für terrestrische
Mikrobiologie in Marburg haben nun entdeckt, dass sogar Proteine fraktale Strukturen besitzen können.

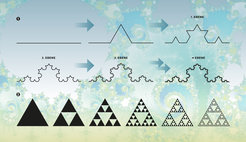
Koch-Kurve und Sierpinski-Dreieck

Die Koch-Kurve (1) beruht auf einer einfachen Regel: Über dem mittleren Drittel einer Strecke werden die Seiten eines gleichschenkligen Dreiecks eingefügt. Wird dieser Vorgang immer wieder wiederholt, entsteht ein an die Struktur einer Schneeflocke erinnerndes Fraktal. Auch das Sierpinski-Dreieck (2) ist ein Fraktal. Es entsteht, wenn man die Mittelpunkte der Seiten eines Dreiecks durch Linien verbindet. So entstehen vier kleinere Dreiecke, von denen das mittlere Teildreieck entfernt wird. Dieses Vorgehen kann beliebig oft auf die übrig gebliebenen Teildreiecke angewandt werden.

Fraktales Protein

Viele Proteine setzen sich aus Untereinheiten zusammen. Die so entstehenden geometrischen Strukturen können zwar regelmäßig angeordnet sein, eine fraktale Geometrie war jedoch bislang noch nie beobachtet worden. Strukturanalysen haben nun ergeben, dass sich bis zu 54 Untereinheiten eines Citrat-Synthase-Enzyms des Cyanobakteriums Synechococcus elongatus so aneinanderlagern können, dass ein Sierpinski-Dreieck entsteht. Die Citrat-Synthase ist ein wichtiger Bestandteil des Stoffwechsels vieler Organismen. Es ist jedoch nur von dieser einen Bakterienart eine solche fraktale Geometrie bekannt – möglicherweise ist sie ein evolutionärer Zufall, der keine besondere Funktion hat.

Natürliche Fraktale

Andere selbstähnliche Objekte in der Natur sind beispielsweise die Blätter von Farnen und Gebirge. Auch in der Architektur können fraktale Strukturen vorkommen. Natürliche Fraktale besitzen jedoch, anders als mathematische Fraktale, nicht unendlich viele selbstähnliche Ebenen.